원주율 π의 정체는?
- 글쓴이
- 최성우
- 등록일
- 2004-11-22 14:42
- 조회
- 21,414회
- 추천
- 23건
- 댓글
- 0건
관련링크
원의 둘레를 지름으로 나눈 값, 즉 원주율이 약 3.14...가 된다는 사실은 초등학교 때부터 배워서 잘 알고 있을 것이다. 원주율을 흔히 π라고 표시하는 이유는 그리스어로 둘레를 뜻하는 ‘περιμετροζ’의 첫 글자에서 따왔기 때문에 누가 처음 사용했는지 확실하지는 않으나 18세기 스위스의 저명한 수학자 겸 물리학자인 ‘오일러(Leonhard Euler; 1707~1783)’가 자신의 저서에서 쓰기 시작한 후부터 다른 학자들도 이 표현을 따랐다고 한다.
그런데 인류가 역사적으로 π의 값을 알아낸 시기와 그 정확도 등을 살펴보는 것은 매우 흥미로울 뿐 아니라, 수학의 발전 역사 혹은 과학사적인 측면에서도 상당한 의미가 있을 듯하다.
성경의 기록을 보면, 구약성서 ‘열왕기상’과 ‘역대하’에 “바다를 부어 만들었으니 지름이 십 규빗(길이의 단위)이요, 그 모양이 둥글고 그 고는 다섯 규빗이며 주위는 삼십 규빗 줄을 두들 만하며...”라고 나와 있는데, 주위를 지름으로 나누면 3이 되므로 기원전 10세기 무렵인 솔로몬 왕 치하에 사용한 원주율 값은 3 정도라는 것을 알 수 있다.
이보다 앞선 기원전 약 1700년 전에 기록되었을 것으로 추측되는 고대 이집트의 책 '린드 파피루스'에는 "원의 넓이를 구하려면, 지름의 9분의 1을 뺀 후 그것을 제곱한다."라고 되어 있는데, 이 방식을 따라서 계산하면 원주율이 약 3.16049... 가 되는 셈이다. 피라미드를 건설했던 고대 이집트 사람들은 실용적인 기하학 지식이 매우 뛰어났음을 짐작할 수 있다.
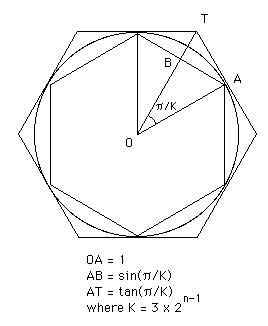
소수 둘째 자리까지의 정확한 원주율을 처음으로 계산해 낸 이는 그리스의 수학자 ‘아르키메데스(Archimedes; B. C. 287?-212)’이다. 여러 일화들을 남긴 이 유명한 수학자는 다각형들을 원에 내접, 외접 시켜가면서 원주율을 계산한 결과, 3과 10/71 보다는 크고, 3과 1/7보다는 작다는 사실을 알았다. 즉 π = 3.14... 라는 값을 밝힌 것이며, 이 근사값은 오늘날까지도 널리 쓰이고 있다.
한편 고대 동양에서도 당시 서양 못지않게 정확한 원주율 값들을 계산한 바 있다. 1세기경에 쓰여 진 것으로 추측되는 고대 중국의 유명한 수학교과서 '구장산술(九章算術)'은 246가지의 예제가 실려 있는 당대 세계 최고 수준의 수학책이라 볼 수 있는데, 초기에 이 책에 나타난 원주율은 약 3 정도였다. 그러나 훗날 구장산술에 주석을 단 수학자 유휘(劉徽)는, 3세기 경에 무한등비급수와 유사한 방법을 적용하여 아르키메데스보다 훨씬 더 정밀한 원주율 값을 계산해 내었다. 또한 6세기 경, 중국 남북조 시대 송(宋)나라의 수학자이자 과학자였던 ‘조충지(祖沖之; 429-500)’는 비슷한 방법으로 π = 3.1415926... 라는 놀랄만한 원주율 값을 계산해 자신의 저서 ‘철술(綴術)’에 기록하였다. 이는 355/113이라는 근사값으로 서양에도 전해졌고, 서양에서는 15세기까지도 이처럼 정확한 원주율 값은 나오지 않았다.
이후 독일의 수학자 ‘루돌프(Ludolph; 1540~1610)’는 거의 평생을 바쳐서 소수점 아래 35자리까지의 원주율을 계산해 바 있는데, 17세기 말엽 ‘뉴턴(Issac Newton; 1642~1727)’과 ‘라이프니츠(Gottfried Wilhelm von Leibniz; 1646~1716)’에 의해 미적분법이 개발된 후, 수학자들은 이를 이용하여 한결 수월하게 원주율을 계산할 수 있었다.
한편 18세기 프랑스의 박물학자 ‘뷔퐁(Georges Louis Leclerc de Buffon; 1707~1788)’은 이른바 ‘바늘문제’라는 독특하고도 흥미로운 원주율 계산법을 제시한 바 있다. 적당한 길이의 바늘을 그 길이의 두 배 간격으로 평행선을 여러 개 그은 종이 위에 충분히 많은 횟수로 떨어뜨리면, 평행선과 바늘이 교차한 횟수와 전체 떨어뜨린 횟수의 비율이 곧 원주율에 근접하게 된다는 것이다. 이 방법은 오늘날 수학이나 물리학 등에서 자주 쓰이는, 확률에 의한 넓이의 계산 방법인 ‘몬테카를로 방법(Monte Carlo method)'과 유사한 면이 있다.
손으로 가장 긴 원주율을 계산해 낸 사람은 영국의 수학자 ‘샹크스(William Shanks; 1812-1882)’로서, 1873년경에 소수점 이하 707자리까지 원주율 값을 계산해 낸 바 있다. 그러나 20세기 이후 이 값을 검산을 해 본 결과, 소수점 이하 528자리까지는 정확히 맞았으나, 그 뒤부터는 틀렸다는 사실이 밝혀졌다.
끝없이 이어지는 원주율의 실체에 대하여 수학자들은 진작부터 의문을 품었는데, 1761년에 ‘람베르트(Johann Heinrich Lambert; 1728-1777)’는 그 값이 무리수임을 밝힌 바 있다. 또한 독일의 ‘린데만((Ferdinand Lindemann; 1852-1939)’은 1882년에 π는 무리수(無理數, Irrational Number)일 뿐만 아니라 ‘초월수(超越數, Transcendental Number)’로서 대수 방정식의 근이나 제곱근의 형태로도 표현할 수 없다는 사실을 증명하여 원주율을 끝자리까지 계산해 내려는 수학자들의 노력을 중단시켰다.
오늘날에는 더 이상 정확한 원주율 값을 계산하려고 노력하는 사람은 거의 없을 것이고, 컴퓨터에 의한 원주율의 계산은 도리어 컴퓨터의 성능을 시험해 보려는 것이 주목적일 것이다. 최근에 일본에서는 컴퓨터로 32억 자리 이상의 원주율을 계산해낸 적도 있다. 또한 실생활에서 필요한 근사치도, 인공위성의 발사와 같은 중대한 경우라도 소수점 다섯째자리에서 반올림한 π = 3.1416 정도면 충분하다고 한다. 그러나 지금의 결과를 얻기까지 수많은 수학자, 과학자들의 피땀 어린 노력이 수천 년 간 이어졌으며, 이는 곧 오늘날의 수학과 과학문명을 이루게 된 한 원동력이 되어 왔음을 잊지 말아야 할 것이다.
매년 3월 14일을 ‘π데이’라고 기념하는 곳이 꽤 있는데, 우리도 3월 14일을 화이트데이보다는 ‘원주율의 날’로 기억하는 것은 어떨까? (글 : 최성우-한국과학기술인연합 운영위원)
그림 위 : 유휘(劉徽)가 주석을 붙인 구장산술(九章算術) 제 1권
그림 아래 : 다각형들을 내, 외접시키는, 아르키메데스에 의한 원주율의 계산방법